GraphX プログラミング ガイド
概要
GraphX はグラフとグラフ並列計算のためのSparkの新しいコンポーネントです。高レベルでは、GraphXは新しいグラフ抽象概念を導入することでSparkのRDDを継承します: 各頂点と辺に所属するプロパティを持つ有向多重グラフグラフ計算をサポートするために、GraphXは基本的な操作(例えば、部分グラフ, 結合頂点 および集約メッセージ) とPregelAPIの最適化された変数を公開します。更に、GraphXはグラフ解析タスクを簡単にするために、グラフアルゴリズムおよびビルダーの増大するコレクションを含んでいます。
開始
始めるために最初にしなければいけないのは、SparkおよびGraphXを以下のようにプロジェクトにインポートすることです:
import org.apache.spark._
import org.apache.spark.graphx._
// To make some of the examples work we will also need RDD
import org.apache.spark.rdd.RDDSpark シェルを使っていない場合は、 SparkContextも必要でしょう。Sparkの開始に関してもっと学びたい場合は、Spark クイックスタートガイドを参照してください。
プロパティ グラフ
プロパティグラフは各頂点と辺に所属するユーザ定義のオブジェクトをもつ有向多重グラフです。有向多重グラフは同じ始点と終点を共有する潜在的な多重平行辺を持つ有向グラフです。平行辺のサポートにより同じ頂点間で複数の関係(例えば、協調ワーカーおよびフレンド)がありえるシナリオのモデル化が簡単になります。各頂点はユニークな 64-bit long 識別子 (VertexID)によって印が付けられます。GraphX は頂点の識別子にどのような順序の制限も押し付けません。同様に、辺は対応する始点と終点の識別子を持ちます。
プロパティグラフは 頂点(VD) および辺 (ED) のタイプ上でパラメータ化されます。各頂点と辺ごとに関係するオブジェクトの種類があります。
GraphXは頂点と辺の種類が基本的なデータタイプの場合には特化した配列の中に格納することでメモリ内の足跡を減らして、表現を最適化します(例えば、int,doubleなど)。
場合によっては同じグラフ内で異なるプロパティタイプをもつ頂点を持つことが望ましいかも知れません。これは継承使って行うことができます。例えば、ユーザと商品を2分グラフとしてモデル化するには、以下のようにしなければならないでしょう:
class VertexProperty()
case class UserProperty(val name: String) extends VertexProperty
case class ProductProperty(val name: String, val price: Double) extends VertexProperty
// The graph might then have the type:
var graph: Graph[VertexProperty, String] = nullRDDのように、プロパティグラフは不変、分散および対障害性があります。グラフの値あるいは構造を変更するには、望ましい変更をした新しいグラフを生成することで行うことができます。元のグラフの本質的な部分(つまり、影響を受けない構造、属性、およびインデックス)は、この本質的な機能データ構造の犠牲を減らした新しいグラフの中で再利用されることに注意してください。グラフは頂点パーティション ヒューリィスティックの分類を使ってexecutorを横断してパーティションされます。RDDと同じように、グラフの各パーティションは障害があった時に異なるマシーンで再生成することができます。
論理的にプロパティグラフは各頂点と辺のプロパティをエンコードしたタイプのコレクション(RDD)のペアに対応します。最終的に、グラフクラスはグラフの頂点と辺にアクセスするためのメンバーを含んでいます。
class Graph[VD, ED] {
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
}クラス VertexRDD[VD] および EdgeRDD[ED] はそれぞれ RDD[(VertexID, VD)] および RDD[Edge[ED]] を継承し最適化されたバージョンです。VertexRDD[VD] とEdgeRDD[ED] はグラフ計算周りに構築された追加の機能を提供し、内部の最適化に利用します。頂点と辺のRDDの章の中で VertexRDD および EdgeRDD API を詳細に議論しますが、今はそれらは単なるRDDの形として考えることができます: RDD[(VertexID, VD)] と RDD[Edge[ED]]。
プロパティ グラフの例
GraphXプロジェクトの様々な協力者からなるプロパティグラフを構築したいとします。頂点のプロパティはユーザ名と業務を含むかも知れません。協力者の間の関係を表す文字列を辺に注釈をつけることができるかも知れません。
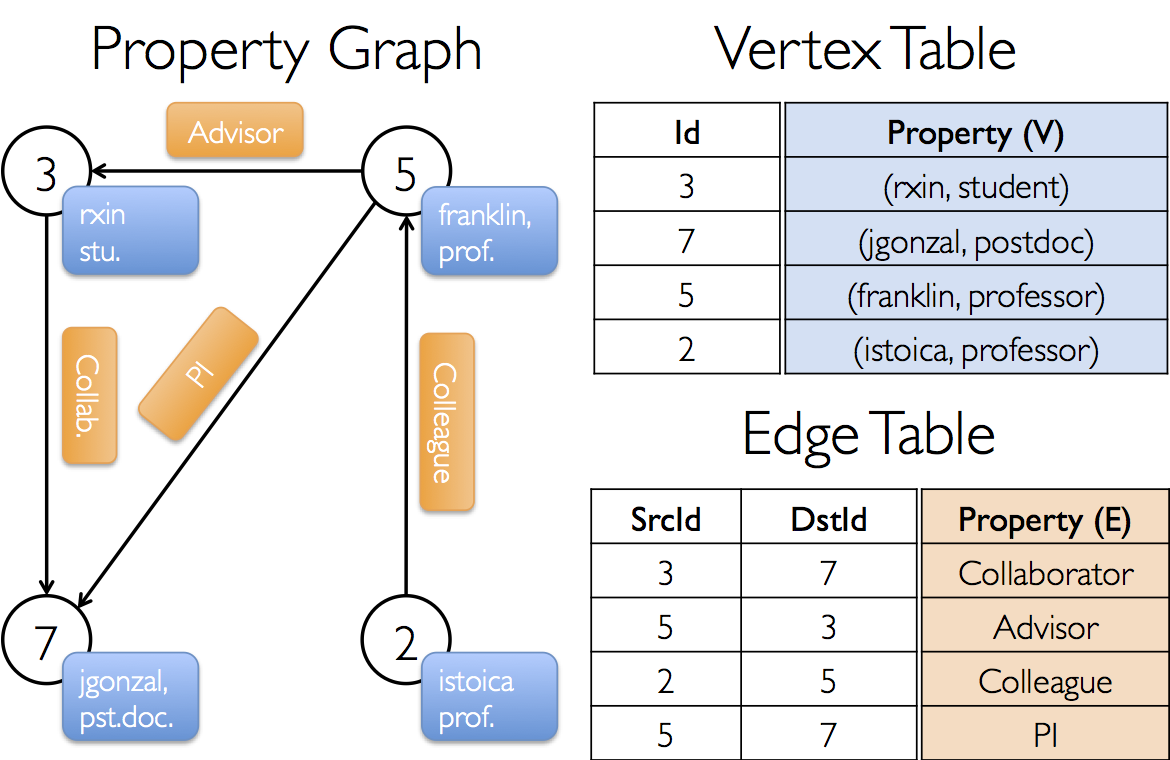
結果のグラフは以下の種類の署名を持つでしょう:
val userGraph: Graph[(String, String), String]生ファイル、RDDおよび同調生成器からでもプロパティグラフを構築する様々な方法があります。graph buildersの章の中で詳細について議論されます。おそらく最も一般的な方法はグラフ オブジェクトを使う方法です。例えば、以下のコードはRDDのコレクションからグラフを構築します:
// Assume the SparkContext has already been constructed
val sc: SparkContext
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Array(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)上の例では、Edge caseクラスを使用します。Edge は始点および頂点の識別子に対応するsrcId とdstId を持ちます。更に、Edge クラスは辺プロパティを格納するattr メンバーを持ちます。
graph.vertices および graph.edges メンバーをそれぞれ使用することで、グラフをそれぞれ頂点および辺ビューに分解することができます。
val graph: Graph[(String, String), String] // Constructed from above
// Count all users which are postdocs
graph.vertices.filter { case (id, (name, pos)) => pos == "postdoc" }.count
// Count all the edges where src > dst
graph.edges.filter(e => e.srcId > e.dstId).count
graph.verticesはRDD[(VertexID, (String, String))]を拡張したVertexRDD[(String, String)]を返すため、集合を分解するためにscalecaseを使用します。一方で、graph.edgesはEdge[String]オブジェクトを含むEdgeRDDを返します。以下のようにしてcase クラスタイプ コンストラクタも使用することができます:
graph.edges.filter { case Edge(src, dst, prop) => src > dst }.countプロパティグラフの頂点および辺ビューに加えて、GraphXはトリプレットビューも公開します。トリプレットビューはEdgeTripletクラスのインスタンスを含むRDD[EdgeTriplet[VD, ED]]がもたらす頂点と辺のプロパティを論理的に結合します。この join は以下のSQL表現で表されます:
SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Idあるいは、以下のようにグラフィカルに:

EdgeTripletクラスはそれぞれ始点および終点プロパティを含むsrcAttr および dstAttrを追加することでEdge クラスを拡張します。ユーザ間の関係を表す文字列のコレクションを描画するためにグラフのトリプレットビューを使うことができます。
val graph: Graph[(String, String), String] // Constructed from above
// Use the triplets view to create an RDD of facts.
val facts: RDD[String] =
graph.triplets.map(triplet =>
triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1)
facts.collect.foreach(println(_))グラフ操作
RDDが map, filter, および reduceByKeyのような基本操作を持つように、プロパティグラフもユーザ定義関数を取り、変換されたプロパティと構造を持つ新しいグラフを生成する基本的な操作のコレクションを持ちます。最適化された実装を持つ中心となる操作は Graphで定義され、基本操作の組み合わせとして表現される便利な操作は GraphOpsで定義されます。しかし、Scalaのimplicitのおかげで GraphOps 内のオペレータは自動的に Graphのメンバーとして利用することができます。例えば、(GraphOpsで定義される)各頂点の角度は以下のように計算することができます:
val graph: Graph[(String, String), String]
// Use the implicit GraphOps.inDegrees operator
val inDegrees: VertexRDD[Int] = graph.inDegreesコア グラフ操作と GraphOpsの間の区別化の理由は、将来異なるグラフ表現をサポートすることができるかどうかということです。各グラフ表現はコア操作の実装を提供し、GraphOpsで定義される便利な操作の多くを最良できなければなりません。
操作の要約リスト
以下は Graph および GraphOps で定義されている機能のクイックサマリーですが、簡単化のためにGraphのメンバーとして表現されています。幾つかの関数の象徴は単純化(例えば、デフォルトの引数と型制限は削除されました)され、幾つかのもっと上級の機能は削除されました。公的な操作のリストについては、APIドキュメントを調べてください。
/** Summary of the functionality in the property graph */
class Graph[VD, ED] {
// Information about the Graph ===================================================================
val numEdges: Long
val numVertices: Long
val inDegrees: VertexRDD[Int]
val outDegrees: VertexRDD[Int]
val degrees: VertexRDD[Int]
// Views of the graph as collections =============================================================
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Functions for caching graphs ==================================================================
def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
def cache(): Graph[VD, ED]
def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]
// Change the partitioning heuristic ============================================================
def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]
// Transform vertex and edge attributes ==========================================================
def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])
: Graph[VD, ED2]
// Modify the graph structure ====================================================================
def reverse: Graph[VD, ED]
def subgraph(
epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
vpred: (VertexID, VD) => Boolean = ((v, d) => true))
: Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]
// Join RDDs with the graph ======================================================================
def joinVertices[U](table: RDD[(VertexID, U)])(mapFunc: (VertexID, VD, U) => VD): Graph[VD, ED]
def outerJoinVertices[U, VD2](other: RDD[(VertexID, U)])
(mapFunc: (VertexID, VD, Option[U]) => VD2)
: Graph[VD2, ED]
// Aggregate information about adjacent triplets =================================================
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexID]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexID, VD)]]
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[A]
// Iterative graph-parallel computation ==========================================================
def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(
vprog: (VertexID, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexID,A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED]
// Basic graph algorithms ========================================================================
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
def connectedComponents(): Graph[VertexID, ED]
def triangleCount(): Graph[Int, ED]
def stronglyConnectedComponents(numIter: Int): Graph[VertexID, ED]
}プロパティの操作
RDDの map オペレータのように、プロパティグラフは以下のものを含んでいます:
class Graph[VD, ED] {
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
}これらの各オペレータはユーザ定義のmap 関数によって修正された頂点あるいは辺のプロパティを使って新しいグラフを取り出します。
各場合においてグラフ構造は影響を受けないことに注意してください。これは、結果のグラフが元のグラフの構造インデックスを再利用できるこれらのオペレータの重要な機能です。. 以下のコード断片は論理的に等価ですが、最初のものは構造インデックスを維持しGraphXシステムの最適化から恩恵を受けないでしょう。
val newVertices = graph.vertices.map { case (id, attr) => (id, mapUdf(id, attr)) }
val newGraph = Graph(newVertices, graph.edges)代わりに、インデックスを維持するには
mapVerticesを使用します:
val newGraph = graph.mapVertices((id, attr) => mapUdf(id, attr))これらのオペレータは特定の計算あるいはプロジェクトを不要なプロパティから離すためにグラフを初期化するためにしばしば使用されます。例えば、頂点プロパティとして次数を減らすグラフがあった場合(後でどのようにそのようなグラフを構築するかを説明します)、ページランクのためにそれを初期化します:
// Given a graph where the vertex property is the out degree
val inputGraph: Graph[Int, String] =
graph.outerJoinVertices(graph.outDegrees)((vid, _, degOpt) => degOpt.getOrElse(0))
// Construct a graph where each edge contains the weight
// and each vertex is the initial PageRank
val outputGraph: Graph[Double, Double] =
inputGraph.mapTriplets(triplet => 1.0 / triplet.srcAttr).mapVertices((id, _) => 1.0)構造的な操作
現在のところ、GraphXは良く使われる構造的なオペレータの簡単なセットのみサポートしており、将来もっと追加するつもりでいます。以下は基本的な構造的なオペレータのリストです。
class Graph[VD, ED] {
def reverse: Graph[VD, ED]
def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,
vpred: (VertexId, VD) => Boolean): Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]
}reverse オペレータは全ての辺の方向が逆になった新しいグラフを返します。これは例えばページランクの逆を計算しようとする時に便利かも知れません。reverseオペレータは、頂点あるいは辺のプロパティを変更せず、あるいは辺の数を変更しないため、データの移動あるいは複製無しに効果的に実装することができます。
subgraph オペレータは頂点と辺の述語を取り、頂点の述語を満足する(trueと評価される)頂点と、辺の述語を満足する辺のみを含むグラフを返し、頂点の述語を満足する頂点を接続します。. subgraph オペレータは、グラフを頂点および関心のある辺に制限、あるいは壊れたリンクを削除する多くの状況に使うことができます。 例えば、以下のコードで壊れたリンクを取り除きます:
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof")),
(4L, ("peter", "student"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Array(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi"),
Edge(4L, 0L, "student"), Edge(5L, 0L, "colleague")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)
// Notice that there is a user 0 (for which we have no information) connected to users
// 4 (peter) and 5 (franklin).
graph.triplets.map(
triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1
).collect.foreach(println(_))
// Remove missing vertices as well as the edges to connected to them
val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing")
// The valid subgraph will disconnect users 4 and 5 by removing user 0
validGraph.vertices.collect.foreach(println(_))
validGraph.triplets.map(
triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1
).collect.foreach(println(_))上の例では頂点の述語のみが提供されていることに注意してください。
subgraphオペレータは、頂点あるいは辺の述語が提供されなかった場合にデフォルトをtrueにします。
maskオペレータは、頂点および辺が入力グラフに見つかったものを含むグラフを返すことでサブグラフを構築します。これは、他の関係するグラフのプロパティを基本とするグラフを制限する subgraphオペレータと結合するために使うことができます。例えば、失われた頂点を持つグラフを使って接続されたコンポーネントを実行し、その答えを有効なサブグラフに制限するかも知れません。
// Run Connected Components
val ccGraph = graph.connectedComponents() // No longer contains missing field
// Remove missing vertices as well as the edges to connected to them
val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing")
// Restrict the answer to the valid subgraph
val validCCGraph = ccGraph.mask(validGraph)groupEdges オペレータはマルチグラフの平行辺(つまり、頂点のペア間の複製辺)を一つにします。多くの数学的応用において、並行な辺は一つの辺に(重み付けを組み合わせて)追加することができ、従ってグラフのサイズを削減します。
Join オペレータ
多くの場合において、グラフを使って外部のコレクション(RDD)からデータをjonする必要があります。例えば、既存のグラフとマージしたい特別なユーザプロパティを持つかも知れません。あるいは、一つのグラフから他のグラフへ頂点プロパティを取り出したいと思うかも知れません。これらのタスクはjoin オペレータを使って行うことができます。以下で主要なjoinパラメータをリスト表示します:
class Graph[VD, ED] {
def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)
: Graph[VD, ED]
def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
}joinVertices オペレータは頂点を入力RDDとjoinし、ユーザ定義の map 関数をjoinされた頂点の結果に適用することで得られた頂点のプロパティを持つ新しいグラフを帰します。RDD内で一致する値を持たない頂点はそれらの元の値を維持します。
RDDが指定された頂点に1つ以上の値を持つ場合は、一つだけが使われるだろうことに注意してください。It is therefore recommended that the input RDD be made unique using the following which will also pre-index the resulting values to substantially accelerate the subsequent join.
val nonUniqueCosts: RDD[(VertexID, Double)]
val uniqueCosts: VertexRDD[Double] =
graph.vertices.aggregateUsingIndex(nonUnique, (a,b) => a + b)
val joinedGraph = graph.joinVertices(uniqueCosts)(
(id, oldCost, extraCost) => oldCost + extraCost)もっと一般的な outerJoinVertices は ユーザ定義のmap関数が全ての頂点に適用されて頂点のプロパティのタイプを変更するという点を除いてjoinVerticesに似た挙動をします。全ての頂点が入力のRDDの値と一致するわけではないので、 map 関数はOption のタイプを取ります。例えば、outDegreeを使って頂点プロパティを初期化することでページランクのグラフをセットアップすることができます。
val outDegrees: VertexRDD[Int] = graph.outDegrees
val degreeGraph = graph.outerJoinVertices(outDegrees) { (id, oldAttr, outDegOpt) =>
outDegOpt match {
case Some(outDeg) => outDeg
case None => 0 // No outDegree means zero outDegree
}
}複数のパラメータリスト(例えば、
f(a)(b))は上の例で使われた関数のパターンを運搬したことに気づいたかも知れません。f(a)(b)をf(a,b)として同等に書ける間は、bがaに依存しないことを型推論することを意味します。結果的に、ユーザはユーザ定義関数について型の注釈を提供する必要があるでしょう。
val joinedGraph = graph.joinVertices(uniqueCosts,
(id: VertexID, oldCost: Double, extraCost: Double) => oldCost + extraCost)近隣集約
多くのグラフ解析タスクでの重要なステップは各兆点についての情報を集約することです。例えば、各ユーザが持っているフォルワーの数あるいは各ユーザのフォロワーの平均年齢を知りたいと思うかも知れません。多くの反復グラフアルゴリズム(例えば、ページランク、最短パス、接続コンポーネント)は隣接する頂点のプロパティを繰り返し集約します(例えば、現在のページランクの値、始点への最短パス、もっとも小さい到達可能な頂点のid)。
パフォーマンスの改善のために、主要な集約オペレータを
graph.mapReduceTripletsから新しいgraph.AggregateMessagesに変更しました。API内の変更は比較的小さいですが、以下に移行のガイドを示します。
集約メッセージ (aggregateMessages)
GraphXのコア集約操作はaggregateMessagesです。このオペレータはユーザ定義のsendMsg 関数をグラフ内の 各edge tripletに適用し、終点の頂点にそれらのメッセージを集約するためにmergeMsg 関数を使用します。
class Graph[VD, ED] {
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[Msg]
}ユーザ定義のsendMsg 関数はEdgeContextを取ります。これは、メッセージを始点および終点の属性に送信するために、辺の属性および関数とともに始点および終点の属性 (sendToSrcおよび sendToDst) を公開します。map-reduce内のmap関数として sendMsgを考えてみてください。ユーザ定義の mergeMsg 関数は同じ頂点へ向かう2つのメッセージを取り、一つのメッセージを生成します。map-reduce内のmap関数として sendMsgを考えてみてください。aggregateMessages オペレータは各頂点に向かう集約メッセージ(タイプはMsg) を含む VertexRDD[Msg] を返します。メッセージを受け取らなかった頂点は返される VertexRDDに含まれません。
更に、 aggregateMessages はどのようなデータがEdgeContextでアクセスされるかを示す任意のtripletsFieldsを取ります(つまり、始点の属性だが終点の属性では無い)。tripletsFieldsの任意のオプションは TripletFields で定義されており、デフォルト値は ユーザ定義のsendMsg関数がEdgeContext内の全てのフィールドにアクセスすることができるTripletFields.All です。tripletFields 引数は、GraphXが最適化されたjoinストラテジを選択できるために EdgeContext の一部分だけが必要とされるだろうことを、GraphXに使えるために使うことができます。例えば、各ユーザのフォロワーの平均年齢を計算する場合に始点フィールドの値のみを必要とするため、始点のフィールドのみが必要だということを示すためにTripletFields.Src を使うでしょう。
GraphXの以前のバージョンで、
TripletFieldsを推測するためにバイトコードの調査をしていましたが、バイトコードの調査が幾分信頼できないものであると分かり、代わりにもっと明示的なユーザの制御を選択しました。
以下の例では、各ユーザの年上のフォロワーの平均年齢を計算するためにaggregateMessagesを使用します。
import org.apache.spark.graphx.{Graph, VertexRDD}
import org.apache.spark.graphx.util.GraphGenerators
// Create a graph with "age" as the vertex property.
// Here we use a random graph for simplicity.
val graph: Graph[Double, Int] =
GraphGenerators.logNormalGraph(sc, numVertices = 100).mapVertices( (id, _) => id.toDouble )
// Compute the number of older followers and their total age
val olderFollowers: VertexRDD[(Int, Double)] = graph.aggregateMessages[(Int, Double)](
triplet => { // Map Function
if (triplet.srcAttr > triplet.dstAttr) {
// Send message to destination vertex containing counter and age
triplet.sendToDst(1, triplet.srcAttr)
}
},
// Add counter and age
(a, b) => (a._1 + b._1, a._2 + b._2) // Reduce Function
)
// Divide total age by number of older followers to get average age of older followers
val avgAgeOfOlderFollowers: VertexRDD[Double] =
olderFollowers.mapValues( (id, value) =>
value match { case (count, totalAge) => totalAge / count } )
// Display the results
avgAgeOfOlderFollowers.collect.foreach(println(_))
aggregateMessagesオペレーションは、メッセージ(およびメッセージの要約)が一定のサイズである場合に最良の機能を果たします(例えば、listと結合の代わりに、floatと追加)。
Map Reduce トリプレット移行ガイド (旧来)
In earlier versions of GraphX neighborhood aggregation was accomplished using the
mapReduceTriplets operator:
class Graph[VD, ED] {
def mapReduceTriplets[Msg](
map: EdgeTriplet[VD, ED] => Iterator[(VertexId, Msg)],
reduce: (Msg, Msg) => Msg)
: VertexRDD[Msg]
}mapReduceTriplets オペレータは、各トリプレットに適用されユーザ定義の reduce 関数を使用して集約するmessages を返すことができるユーザ定義のmap関数を取ります。しかし、返されたイテレータの使用が高くつき、そして能力を追加の最適化に適用することを抑制すると分かりました(例えば、頂点の再番号付け)。aggregateMessagesでは、tripletフィールドを公開するEdgeContextを導入し、元および宛先の頂点へ明示的にメッセージを送信する機能も導入しました。更に、バイトコードの調査を削除し、代わりにtriplet内のどのフィールドが実際に必要なのかをユーザが指定することを要求します。
以下のコードブロックはmapReduceTripletsを使用します:
val graph: Graph[Int, Float] = ...
def msgFun(triplet: Triplet[Int, Float]): Iterator[(Int, String)] = {
Iterator((triplet.dstId, "Hi"))
}
def reduceFun(a: String, b: String): String = a + " " + b
val result = graph.mapReduceTriplets[String](msgFun, reduceFun)下のようにaggregateMessages を使って書き換えることができます:
val graph: Graph[Int, Float] = ...
def msgFun(triplet: EdgeContext[Int, Float, String]) {
triplet.sendToDst("Hi")
}
def reduceFun(a: String, b: String): String = a + " " + b
val result = graph.aggregateMessages[String](msgFun, reduceFun)次数情報の計算
一般的な集約タスクは各頂点の次数を計算します: 各頂点に隣接している辺の数。有向グラフのコンテキストでは、各頂点の入次数、出次数、総次数を知ることがしばしば必要になります。GraphOpsクラスは各頂点の次数を計算するためのオペレータのコレクションを含んでいます。例えば、以下では最大の入次数、出次数、総次数を計算します:
// Define a reduce operation to compute the highest degree vertex
def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {
if (a._2 > b._2) a else b
}
// Compute the max degrees
val maxInDegree: (VertexId, Int) = graph.inDegrees.reduce(max)
val maxOutDegree: (VertexId, Int) = graph.outDegrees.reduce(max)
val maxDegrees: (VertexId, Int) = graph.degrees.reduce(max)近傍の収集
場合によっては、近傍頂点とそれらの属性を各頂点で集めることで、計算を表すことがもっと簡単になるかも知れません。これはcollectNeighborIds および collectNeighbors オペレータを使って簡単に行うことができます。
class GraphOps[VD, ED] {
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[ Array[(VertexId, VD)] ]
}これらのオペレータは情報を複製しかなりの通信を必要とするため、とてもコストが高いものになりえます。可能であれば、同じ計算を直接
aggregateMessagesオペレータを使って表現してみてください。
キャッシュと非キャッシュ
Sparkでは、RDDはデフォルトではメモリ内に永続しません。再計算を避けるために、それらを複数回使う場合は明示的にキャッシュされなければなりません(Spark プログラミング ガイドを見てください)。GraphXのグラフも同じ挙動をします。グラフを複数回使用する場合は、最初にGraph.cache() を呼ぶようにしてください。
繰り返しの計算時には、uncaching もベストパフォーマンスのために必要かも知れません。デフォルトでは、キャッシュされたRDDとグラフは、メモリの圧迫がそれらをLRU順に追い出すまでメモリ内に残ります。繰り返しの計算時には、以前の繰り返しの中間結果がキャッシュを満たしているでしょう。最終的にそれらは追い出されるでしょうが、メモリ内の不要なデータはガベージコレクションを遅くするでしょう。中間結果が不要になったらすぐにキャッシュしなくすることは効果的でしょう。これには、各繰り返しにおいてグラフあるいはRDDの実体化(キャッシュおよび施行)、他の全てのデータセットの非キャッシュ化、そして後の繰り替えでの実体化されたデータセットの使用を必要とします。しかし、グラフは複数のRDDからなるためそれらを正確に非永続化することは難しいです。繰り返し計算にはPregel APIを使うことをお勧めします。それは正確に中間結果を非永続化します。
Pregel API
Graphは近傍のプロパティに依存する頂点のプロパティとして本質的に再帰的なデータ構造です。そして近傍のプロパティは、それらの近傍のプロパティに依存します。結果として多くの重要なグラフアルゴリズムは、あらかじめ決まった条件に達するまで、各要点のプロパティを繰り返し再計算します。さまざまなgraph-parallel 抽出が、それらの繰り返しアルゴリズムを表現するために提案されています。GraphXはPregel APIの変数を公開します。
高レベルにおいて、GraphXのPregelオペレータはグラフの位相幾何学に束縛されたバルク同期並行メッセージ抽象です。Pregelオペレータは、以前のスーパーステップからの入力メッセージの概要を受け取る頂点内の一連のスーパーステップの中で実行され、頂点のプロパティのために新しい値を計算し、次のスーパーステップで近傍の頂点へメッセージを送信します。Pregelと違い、メッセージは辺トリプレットとして並行して計算され、メッセージの計算は始点と終点の頂点の属性の両方にアクセスします。メッセージを受け取らなかった頂点はスーパーステップの中でスキップされます。Pregelオペレータは繰り返しを終了し、メッセージが残っていない場合は最後のグラフを返します。
多くの標準的なPregel実装と異なり、GraphXの頂点は隣接する頂点にのみメッセージを送信することができ、ユーザ定義のメッセージ関数を使って並行してメッセージの構築が行われます。これらの制限によりGraphX内で更に最適化が可能です。
以下はPregel オペレータのタイプシグネチャーと、その実装の概略です (graph.cacheへの呼び出しは削除されたことに注意してください):
class GraphOps[VD, ED] {
def pregel[A]
(initialMsg: A,
maxIter: Int = Int.MaxValue,
activeDir: EdgeDirection = EdgeDirection.Out)
(vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED] = {
// Receive the initial message at each vertex
var g = mapVertices( (vid, vdata) => vprog(vid, vdata, initialMsg) ).cache()
// compute the messages
var messages = g.mapReduceTriplets(sendMsg, mergeMsg)
var activeMessages = messages.count()
// Loop until no messages remain or maxIterations is achieved
var i = 0
while (activeMessages > 0 && i < maxIterations) {
// Receive the messages and update the vertices.
g = g.joinVertices(messages)(vprog).cache()
val oldMessages = messages
// Send new messages, skipping edges where neither side received a message. We must cache
// messages so it can be materialized on the next line, allowing us to uncache the previous
// iteration.
messages = g.mapReduceTriplets(
sendMsg, mergeMsg, Some((oldMessages, activeDirection))).cache()
activeMessages = messages.count()
i += 1
}
g
}
}Pregelタスクは2つの引数リスト(つまり、graph.pregel(list1)(list2))を取ることに注意してください。最初の引数のリストは初期メッセージを含む設定パラメータ、繰り返しの最大数、およびメッセージを送信する辺の方向(デフォルトは頂点を出る方向)を含みます。二つ目の引数のリストはメッセージを受け取るためのユーザ定義の関数(頂点プログラムvprog)、メッセージの計算(sendMsg)、およびメッセージの組み合わせmergeMsgを含みます。
以下の例の一つの始点の最短パスのような計算の表現をするためにPregelオペレータを使うことができます。
import org.apache.spark.graphx.{Graph, VertexId}
import org.apache.spark.graphx.util.GraphGenerators
// A graph with edge attributes containing distances
val graph: Graph[Long, Double] =
GraphGenerators.logNormalGraph(sc, numVertices = 100).mapEdges(e => e.attr.toDouble)
val sourceId: VertexId = 42 // The ultimate source
// Initialize the graph such that all vertices except the root have distance infinity.
val initialGraph = graph.mapVertices((id, _) =>
if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
(id, dist, newDist) => math.min(dist, newDist), // Vertex Program
triplet => { // Send Message
if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
} else {
Iterator.empty
}
},
(a, b) => math.min(a, b) // Merge Message
)
println(sssp.vertices.collect.mkString("\n"))
Graph ビルダー
GraphXはRDD内あるいはディスク上の頂点および辺のコレクションからグラフを構築する幾つかの方法を提供します。デフォルトではグラフビルダーはグラフの辺を再分割しません; それどころか、(HDFS内の元のブロックのように)辺はデフォルトのパーティションのままです。同一の辺は同じパーティションに配置されると仮定するため、Graph.groupEdges はグラフが再パーティションされることを必要とします。つまり、groupEdgesが呼ばれる前に Graph.partitionByを呼ぶ必要があります。
object GraphLoader {
def edgeListFile(
sc: SparkContext,
path: String,
canonicalOrientation: Boolean = false,
minEdgePartitions: Int = 1)
: Graph[Int, Int]
}GraphLoader.edgeListFileはディスク上の辺のリストからグラフをロードする方法を提供します。#で始まるコメント行をスキップして、以下の形式の隣接リスト(始点ID, 終点ID) のペアをパースします。:
# This is a comment
2 1
4 1
1 2
辺によって言及される全ての頂点を自動的に作成しながら、指定された辺からGraph を作成します。全ての頂点と辺の属性は、1がデフォルトです。canonicalOrientation 引数は正の方向(srcId < dstId)に辺を向けることができます。これはconnected components アルゴリズムによって必要とされます。minEdgePartitions 引数は生成する辺パーティションの最少数を指定します; 例えばHDFSファイルがもっとブロックを持つ場合、指定よりも多い辺のパーティションがあるかもしれません。
object Graph {
def apply[VD, ED](
vertices: RDD[(VertexId, VD)],
edges: RDD[Edge[ED]],
defaultVertexAttr: VD = null)
: Graph[VD, ED]
def fromEdges[VD, ED](
edges: RDD[Edge[ED]],
defaultValue: VD): Graph[VD, ED]
def fromEdgeTuples[VD](
rawEdges: RDD[(VertexId, VertexId)],
defaultValue: VD,
uniqueEdges: Option[PartitionStrategy] = None): Graph[VD, Int]
}Graph.apply は頂点と辺のRDDからグラフを生成することができます。デュプリケートされた頂点は任意に取り上げられ、辺のRDD内で見つかったが頂点RDDでは無い頂点はデフォルトの属性が割り当てられます。
Graph.fromEdges は、辺によって述べられた頂点を自動的に生成し、それらにデフォルトの値を割り当てて、辺のRDDのみからグラフを生成することができます。
Graph.fromEdgeTuples は、辺の値を1に割り当て、辺によって述べられた頂点を自動的に生成し、そらにデフォルトの値を割り当て、辺のRDDのみからグラフを生成することができます。. 辺のデュプリケートもサポートします; デュプリケートするには、いくつかのPartitionStrategyをuniqueEdgesパラメータとして渡します(例えば、uniqueEdges = Some(PartitionStrategy.RandomVertexCut))。それらがデュプリケートできるように、同じパーティションに同一の辺を配置するパーティション戦略が必要です。
頂点と辺のRDD
GraphX は グラフ内に格納されている頂点と辺のRDD ビューを公開します。GraphXは最適化されたデータ構造内に頂点と辺を維持し、それらのデータ構造は追加の機能を提供しますが、頂点と辺は それぞれVertexRDD と EdgeRDD として返されます。この章ではこれらの種類の追加の便利な機能の幾つかを見直します。
頂点のRDD
VertexRDD[A] は RDD[(VertexID, A)] を拡張子、各VertexIDが 一度だけ起きるという追加の制約を追加したものです。更に、 VertexRDD[A]は各頂点がタイプAの属性を持つ セット を表します。内部的には、これは頂点の属性を再利用可能なハッシュマップのデータ構造に格納することで達成されています。結果として、もし2つのVertexRDDが同じ基本の VertexRDD から派生した場合(例えば、filter あるいは mapValues)、それらはハッシュの評価無しに一定時間でjoinされるでしょう。このインデックスされたデータの構造を使うために、VertexRDDが以下の追加の機能を公開します:
class VertexRDD[VD] extends RDD[(VertexID, VD)] {
// Filter the vertex set but preserves the internal index
def filter(pred: Tuple2[VertexId, VD] => Boolean): VertexRDD[VD]
// Transform the values without changing the ids (preserves the internal index)
def mapValues[VD2](map: VD => VD2): VertexRDD[VD2]
def mapValues[VD2](map: (VertexId, VD) => VD2): VertexRDD[VD2]
// Show only vertices unique to this set based on their VertexId's
def minus(other: RDD[(VertexId, VD)])
// Remove vertices from this set that appear in the other set
def diff(other: VertexRDD[VD]): VertexRDD[VD]
// Join operators that take advantage of the internal indexing to accelerate joins (substantially)
def leftJoin[VD2, VD3](other: RDD[(VertexId, VD2)])(f: (VertexId, VD, Option[VD2]) => VD3): VertexRDD[VD3]
def innerJoin[U, VD2](other: RDD[(VertexId, U)])(f: (VertexId, VD, U) => VD2): VertexRDD[VD2]
// Use the index on this RDD to accelerate a `reduceByKey` operation on the input RDD.
def aggregateUsingIndex[VD2](other: RDD[(VertexId, VD2)], reduceFunc: (VD2, VD2) => VD2): VertexRDD[VD2]
}例えば、filter オペレータがどのようにVertexRDDを返すかに注意してください。Filterは実際のところはBitSetを使って実装されており、したがってインデックスの再利用と他のVertexRDDとの高速なjoinを行う能力を維持しています。その上、mapValues オペレータはmap 関数がVertexID を変更することを許可しないため、同じHashMapデータ構造の再利用が有効にされます。同じHashMapから派生した2つのVertexRDDをjoinする場合、leftJoin と innerJoin の両方が識別可能で、コストの掛かるポイントの照合ではなく線形走査によってjoinを実装します。
aggregateUsingIndex オペレータは新しいVertexRDDをRDD[(VertexID, A)]から効率よく構築するのに役立ちます。結果として、もし一連の頂点上にVertexRDD[B]を構築し、なんらかのRDD[(VertexID, A)]の中で頂点のスーパーセットである場合、RDD[(VertexID, A)]の集約と結果のインデックスの両方を再利用することができます。例えば:
val setA: VertexRDD[Int] = VertexRDD(sc.parallelize(0L until 100L).map(id => (id, 1)))
val rddB: RDD[(VertexId, Double)] = sc.parallelize(0L until 100L).flatMap(id => List((id, 1.0), (id, 2.0)))
// There should be 200 entries in rddB
rddB.count
val setB: VertexRDD[Double] = setA.aggregateUsingIndex(rddB, _ + _)
// There should be 100 entries in setB
setB.count
// Joining A and B should now be fast!
val setC: VertexRDD[Double] = setA.innerJoin(setB)((id, a, b) => a + b)辺のRDD
RDD[Edge[ED]]を拡張した EdgeRDD[ED]は、PartitionStrategyの中で定義された様々なパーティションの戦略の一つを使ってパーティションされたブロックの辺を組織化します。各パーティションの中で、辺の続と近傍構造は、個々に属性値を変更する時に最大限再利用できるように格納されます。
EdgeRDDによって公開される3つの追加の関数は以下の通りです:
// Transform the edge attributes while preserving the structure
def mapValues[ED2](f: Edge[ED] => ED2): EdgeRDD[ED2]
// Reverse the edges reusing both attributes and structure
def reverse: EdgeRDD[ED]
// Join two `EdgeRDD`s partitioned using the same partitioning strategy.
def innerJoin[ED2, ED3](other: EdgeRDD[ED2])(f: (VertexId, VertexId, ED, ED2) => ED3): EdgeRDD[ED3]ほとんどのアプリケーションにおいて、EdgeRDD上の操作はグラフ操作によって完遂されるか、RDD クラスに基づいて定義された操作を頼りにすることが分かりました。
最適化された表現
分散されたグラフのGraphX表現の中で使用される最適化の詳細な説明はこのガイドの範囲を超えますが、いくらかの高レベルの理解はAPIの最適な使用とどうようにスケーラブルなアルゴリズムの設計の助けになるかも知れません。GraphX は分散されたグラフのパーティションのために、頂点を切り落とす方法を適用します:
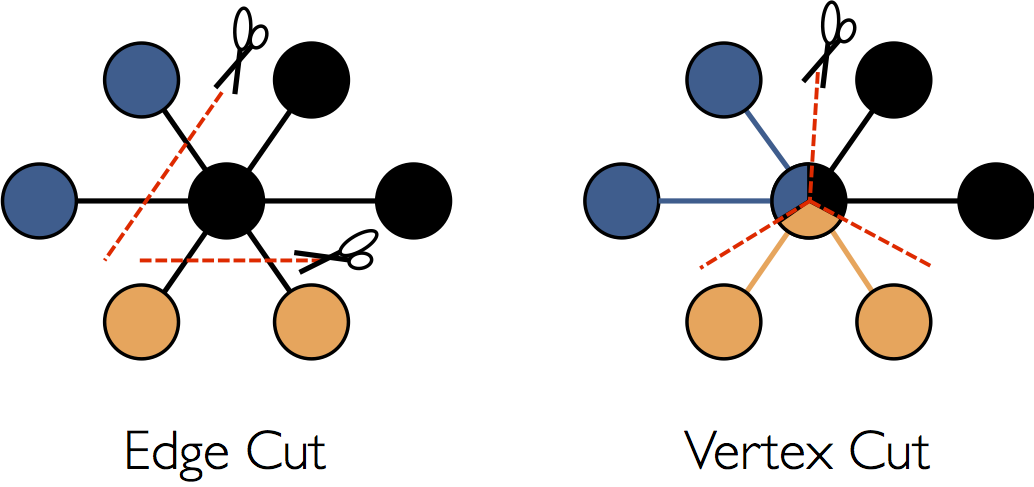
GraphXは、辺に沿ってグラフを分割するのではなく、通信およびストレージのオーバーヘッドの両方を削減できる頂点に沿って分割します。論理的には、これは辺をマシーンに割り当てて、頂点を複数のマシーンをつなぐことができるようにすることに対応します。辺を割り当てる正確な方法はPartitionStrategy に依存し、様々な発見的教授法への幾つかのトレードオフがあります。ユーザはGraph.partitionBy オペレータを使ってグラフを再分割することで異なるストラテジを選択することができます。デフォルトのパーティションストラテジは辺の初期パーティションをグラフの構築時に提供されたものとして使用します。しかし、ユーザは簡単に2DパーティションあるいはGraphXに含まれる他の発見的な方法に切り替えることができます。
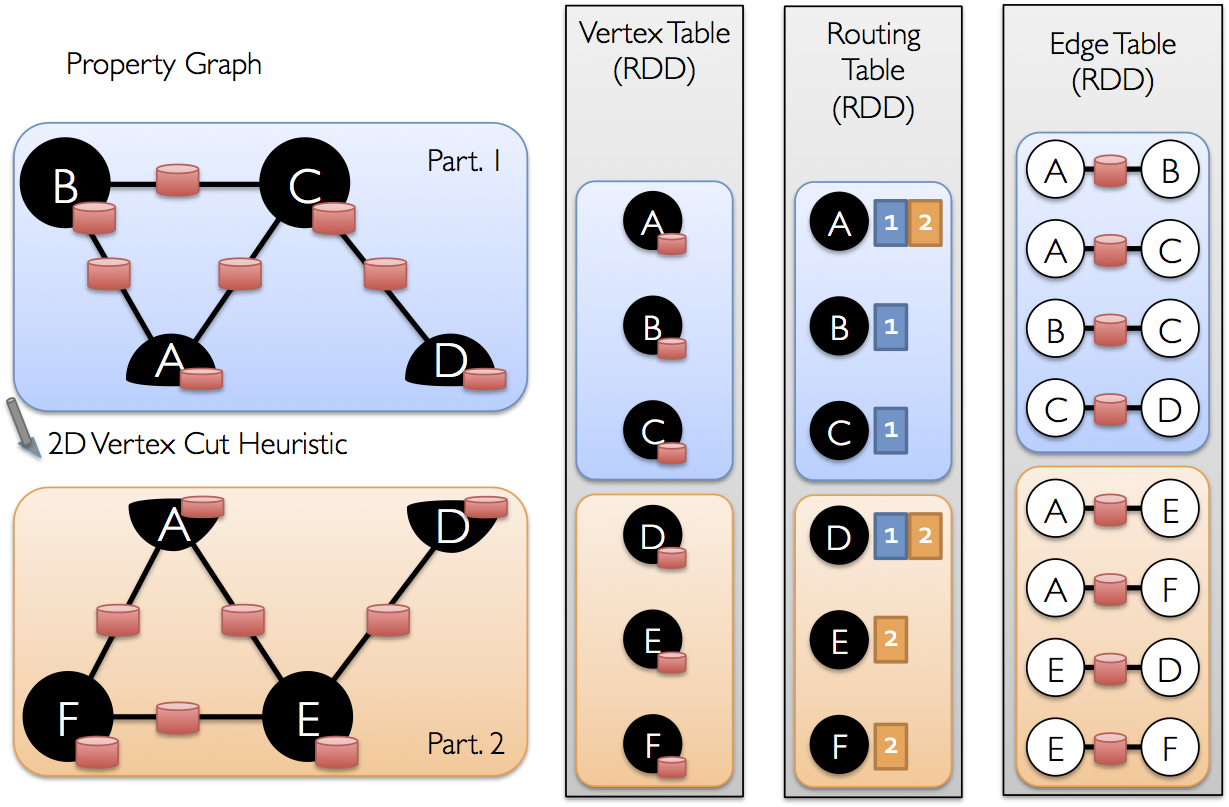
一度辺がパーティションされると、効率的なグラフ並行計算の主要な課題は、辺を持つ頂点の属性の効率的な結合になります。実際の世界のグラフは一般的に頂点よりも多くの辺を持つため、頂点の属性を辺に移動します。全てのパーティションが全ての頂点と隣りあう辺を持つわけでは無いため、triplets および aggregateMessagesのような操作に必要となるjoinを実装する時にどこに頂点をブロードキャストするかを決めるルーティングテーブルを内部的に整備します。
グラフ アルゴリズム
GraphX はタスクの解析を単純化するためのグラフのアルゴリズムのセットを含んでいます。アルゴリズムは org.apache.spark.graphx.lib パッケージの中に含まれており、GraphOpsを通じてGraph上のメソッドとして直接アクセスすることができます。この章ではアルゴリズムとそれがどうやって使われるかについて説明します。
ページランク
u から v への辺がuによってvの推奨を表すとして、PageRankはグラフ内の各頂点の重要度を測定します。例えば、Twitterのユーザが多くの他の人にフォローされている場合、そのユーザは高くランクされているでしょう。
GraphXにはPageRank オブジェクトのメソッドとしてPageRankの静的および動的な実装が付属しています。静的 PageRankはある繰り返しの数の間実行し、一方で動的PgeRankはランクが収束するまで実行します(つまり、ある許容範囲によって変更を停止します)。GraphOpsを使ってGraph上のメソッドとして直接アルゴリズムを呼び出すことができます。
GraphXはPageRankを実行できるソーシャルネットワークデータセットの例も含んでいます。ユーザのセットは data/graphx/users.txtの中で与えられ、ユーザ間の関係のセットはdata/graphx/followers.txtの中で与えられます。以下のようにして各ユーザのページランクを計算します:
import org.apache.spark.graphx.GraphLoader
// Load the edges as a graph
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Run PageRank
val ranks = graph.pageRank(0.0001).vertices
// Join the ranks with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val ranksByUsername = users.join(ranks).map {
case (id, (username, rank)) => (username, rank)
}
// Print the result
println(ranksByUsername.collect().mkString("\n"))
連結コンポーネント
接続されたコンポーネントアルゴリズムはグラフの各接続されたコンポーネントを頂点の最も小さい数字のIDでラベル付けします。例えば、ソーシャルネットワークの中で、接続されたコンポーネントはクラスタを見積もることができます。GraphXはConnectedComponents オブジェクトの中のアルゴリズムの実装を含み、以下のようにしてPageRank の章の例のソーシャルネットワークのデータセットの接続されているコンポーネントを計算します:
import org.apache.spark.graphx.GraphLoader
// Load the graph as in the PageRank example
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Find the connected components
val cc = graph.connectedComponents().vertices
// Join the connected components with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val ccByUsername = users.join(cc).map {
case (id, (username, cc)) => (username, cc)
}
// Print the result
println(ccByUsername.collect().mkString("\n"))
三角形数え上げ
頂点が2つの近接頂点とそれらの間の辺を持つ場合、頂点は三角形の一部です。GraphXはクラスタリングの計測を提供して、各頂点を経由する三角形の数を決定する TriangleCount オブジェクト の中に三角形数え上げアルゴリズムを実装します。PageRank sectionからソーシャルネットワークデータセットの三角形のカウントを計算します。TriangleCountは辺が正式な方向(srcId < dstId)にあり、グラフがGraph.partitionByを使ってパーティションされることを必要とすることに注意してください。
import org.apache.spark.graphx.{GraphLoader, PartitionStrategy}
// Load the edges in canonical order and partition the graph for triangle count
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt", true)
.partitionBy(PartitionStrategy.RandomVertexCut)
// Find the triangle count for each vertex
val triCounts = graph.triangleCount().vertices
// Join the triangle counts with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val triCountByUsername = users.join(triCounts).map { case (id, (username, tc)) =>
(username, tc)
}
// Print the result
println(triCountByUsername.collect().mkString("\n"))
例
幾つかのテキストファイルからグラフを構築したいとします。グラフを重要な関係とユーザに制限し、サブグラフ上でページランクを実行し、最後にトップユーザと関連する属性を返します。これの全てをGraphXを使って単に数行で行うことができます:
import org.apache.spark.graphx.GraphLoader
// Load my user data and parse into tuples of user id and attribute list
val users = (sc.textFile("data/graphx/users.txt")
.map(line => line.split(",")).map( parts => (parts.head.toLong, parts.tail) ))
// Parse the edge data which is already in userId -> userId format
val followerGraph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Attach the user attributes
val graph = followerGraph.outerJoinVertices(users) {
case (uid, deg, Some(attrList)) => attrList
// Some users may not have attributes so we set them as empty
case (uid, deg, None) => Array.empty[String]
}
// Restrict the graph to users with usernames and names
val subgraph = graph.subgraph(vpred = (vid, attr) => attr.size == 2)
// Compute the PageRank
val pagerankGraph = subgraph.pageRank(0.001)
// Get the attributes of the top pagerank users
val userInfoWithPageRank = subgraph.outerJoinVertices(pagerankGraph.vertices) {
case (uid, attrList, Some(pr)) => (pr, attrList.toList)
case (uid, attrList, None) => (0.0, attrList.toList)
}
println(userInfoWithPageRank.vertices.top(5)(Ordering.by(_._2._1)).mkString("\n"))
